最近、桐のまな板(安売り)を衝動買いした米澤です。野菜を切るたびにすごくいい音がして癒やされています。
ウェブマーケティングに関わっていると避けて通れないのがABテスト。
このABテストの「結果の信ぴょう性」についてちゃんと考えたことがありますか?
ABテストをやってみた、違いが出た、よし!数字が大きかった方を選ぼう!ってなると思いますが、数字が違うからって必ずしも結果に意味があるとは限りません。
これは統計学と関わってきますが、統計学ってなんか難しいし、意味分からない!実際、ネットで探しても途中で意味がチンプンカンプンになる!
というような、どちらかというと統計学が苦手な人のために、ABテストの統計学を分かりやすく解説します!
しかも!結局統計学の意味が分からなかったとしても、ABテストに本当に意味があったかどうか、分かるようになるので、最後までお付き合いください。
(ヒント:ここから先のお話が一切理解できなくても、自動的に計算してくれるツールがあります!)
どこまでが「誤差」の範囲内?
例えばウェブサイトを例に考えてみます。

内容は全く同じだけれど、あるボタンのデザインだけを変えたページAとページBを用意し、それぞれランダムにユーザーを誘導してABテストを実施したとします。
どちらのデザインだとクリックされやすいのか、調べたいというわけです。
結果は以下のようになりました。
| ページビュー数 | クリック数 | クリック率 | |
|---|---|---|---|
| ページA | 60 | 6 | 10% |
| ページB | 40 | 3 | 7.5% |
一見、ページAの方がかなりクリック率が良いように見えますが、ページBもクリック数がもう1件増えるとクリック率が10%になり、ページAと同じになります。
このデータを見て「ページBはクリック率が低いからページAと比べて全然ダメ」と言う人はほとんどいないと思います。
「クリック数たった1の差なんて、誤差の範囲内じゃん」というのが一般的な反応ではないでしょうか。
でも、この「誤差の範囲内」ってすごい抽象的な表現だと思いませんか?
「データがどれくらいの大きさであれば、「誤差の範囲内」じゃないと言えるのでしょうか。
意味のあるABテストか知るためにまず「期待値」を知る
意味のあるABテストかどうかは、誤差に対する理解が大事になりますが、そのためにはまず誤差の基準となる数字を考えないといけません。
これを「期待値」と言いますが、何を期待しているかというと「AパターンとBパターンには統計的な差がないとしたら、このぐらいの数字が出ることが期待されるよね」という意味です。
実際に観測したデータをもう1回、見てみましょう。
| クリックなし | クリックあり | 合計 (ページビュー数) |
|
|---|---|---|---|
| ページA | 54 | 6 | 60 |
| ページB | 37 | 3 | 40 |
観測したデータの「合計」を算出します(足し上げているだけです)。
| クリックなし | クリックあり | 合計 (ページビュー数) |
|
|---|---|---|---|
| ページA | 54 | 6 | 60 |
| ページB | 37 | 3 | 40 |
| 合計 | 91 | 9 | 100 |
ページAのページビューは全体の60%です。
ページBのページビューは全体の40%です。
今回、数字を分かりやすくするためにページビューとパーセンテージが同じになるようにしていますが、意味は分かりますよね。
ということは、仮説として、ページAのパターンも、ページBのパターンも、どちらも同じだけの確率で反応をされるのであれば、母数が違っていても割り戻せばクリック数は同じになるはずです。
その実際の割り戻しの計算をしてみましょう。
まずページAの「クリックなし」です。
クリックをしなかった人の総数は91人です。
ページAは全体のページビューの60%です。
ということは91人を60%で割り戻すと、期待される「クリックなし」の期待値は54.6となります。
| クリックなし | クリックあり | 合計 (ページビュー) |
クリックなしの期待値 | クリックありの期待値 | |
|---|---|---|---|---|---|
| ページA | 54 | 6 | 60 | 54.6 | |
| ページB | 37 | 3 | 40 | ||
| 合計 | 91 | 9 | 100 |
同じように、クリックした人の総数9人を60%すると、5.4になります。
| クリックなし | クリックあり | 合計 (ページビュー) |
クリックなしの期待値 | クリックありの期待値 | |
|---|---|---|---|---|---|
| ページA | 54 | 6 | 60 | 54.6 | 5.4 |
| ページB | 37 | 3 | 40 | ||
| 合計 | 91 | 9 | 100 |
この要領で、ページBも計算します。
クリックしなかった人の総数91人を、ページBを見た人の割合の40%で割戻すと36.4になります。
| クリックなし | クリックあり | 合計 (ページビュー) |
クリックなしの期待値 | クリックありの期待値 | |
|---|---|---|---|---|---|
| ページA | 54 | 6 | 60 | 54.6 | 5.4 |
| ページB | 37 | 3 | 40 | 36.4 | 3.6 |
| 合計 | 91 | 9 | 100 |
全部計算するとこうなります。
| クリックなし | クリックあり | 合計 (ページビュー) |
クリックなしの期待値 | クリックありの期待値 | |
|---|---|---|---|---|---|
| ページA | 54 | 6 | 60 | 54.6 | 5.4 |
| ページB | 37 | 3 | 40 | 36.4 | 3.6 |
| 合計 | 91 | 9 | 100 |
ページAのクリックなしは54人ですが、ページAとBに差がなかったと仮定した場合に期待されるクリックなしの数は54.6人で、僅かに差があります。
問題は、その「差」というのが有意(「意」味が「有」る)レベルかどうか、ですよね。その計算方法も教えます!
「カイ二乗検定」とやらを使いこなす!
難しいことは抜きにします、というお約束を守るために、この「カイ二乗(X2)検定」が「一体何ものなのか、統計学的にどうして意味があるのか」は、ぜ〜んぶ割愛しちゃいます。
必要なのは、実際に計測した数値から期待していた数値を引いた値を二乗し、期待値で割ったものの合計……
訳が分からないので、実際に何を代入するのか書きます!
もう一回、期待値を計算した表を見てみましょう。
| クリックなし | クリックあり | 合計 (ページビュー) |
クリックなしの期待値 | クリックありの期待値 | |
|---|---|---|---|---|---|
| ページA | 54 | 6 | 60 | 54.6 | 5.4 |
| ページB | 37 | 3 | 40 | 36.4 | 3.6 |
| 合計 | 91 | 9 | 100 |
まずは「ページA」の「クリックなし」に基づく数式。
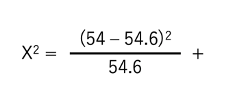
| クリックなし | クリックあり | 合計 (ページビュー) |
クリックなしの期待値 | クリックありの期待値 | |
|---|---|---|---|---|---|
| ページA | 54 | 6 | 60 | 54.6 | 5.4 |
| ページB | 37 | 3 | 40 | 36.4 | 3.6 |
| 合計 | 91 | 9 | 100 |
続いて同じく「ページA」の「クリックあり」に基づく数式。
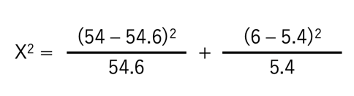
「ページB」の「クリックなし」と「クリックあり」も加えましょう。
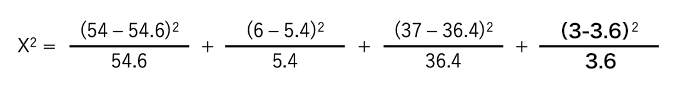
X2=0.183150183
次は「自由度」の計算をします。
はい、もう、自由度が何かとか、気にしないでください。
自由度とは、「行の数」から1を引いた数字と、「列の数」から1を引いた数字を掛け算した数字です。
今回でいうところの「クリックなし」と「クリックあり」が列。
「ページA」と「ページB」が行。
ということは……
自由度= (2-1)*(2-1) = 1
すみません、事例が超シンプルなので、自由度の計算も馬鹿にしているのか!みたいな計算になっていますが、もっと複雑なテストをする場合には役立ちます。
で、この自由度が何を意味するのか、もちろん数学的にも統計学的にもちゃんと説明できますが、今回のブログではカット!!
大事なのはこの数字を使って何をするか、です。
統計的有意性があるか判断するのがp値
自由度の値とカイ二乗値から「p値」というのを計算します。
そして、この「p値」が5%よりも小さかった場合、それは「偶然」ではない!ということに。
5%よりも大きければ「単なる偶然だね」ということになります。
やっと核心をついたところで、残念なお知らせです。
ここまでやってきた数字は全部簡単な数学というか、算数レベルで解けるのですが、「自由度」と「カイ二乗値」から「p値」を計算するのは、全然算数レベルの話では片付けられず、ここで説明するのは不可能です!\(^-^)/
が!!世の中には超便利なツール「エクセル」というものがありまして。
さらに超便利な関数があります!!
= CHISQ.DIST.RT(カイ二乗値,自由度の値)
で計算してくれちゃいます!
今回の場合、
= CHISQ.DIST.RT(0.183150183,1)
とすると!
66.87%という数字が出ました!
66.87%は5%より著しく大きい数字なので、結論として「超!何の疑い様もなく!単なる偶然の産物なのでABテストとしては何の参考にもならない!」ということになりました。
さて、最後にここまで読んだ(あるいは読み飛ばした)方のために。
ルシダス謹製、ABテストの有意性検証をするエクセルシートがダウンロードできます!
実施したABテストの結果を打ち込むだけで勝手に計算してくれて、上記のロジックなんてさ〜っぱり分からなくてもドヤ顔で「統計的有意性があります(ドヤ)って言えるようになりますよ!
メルマガ登録
マーケターやマーケティングにご興味のある方へ。些細なことから「おっ」と思う注目の事柄まで、読んでお得な情報をメールで配信中!気になる方は今すぐご登録を!

